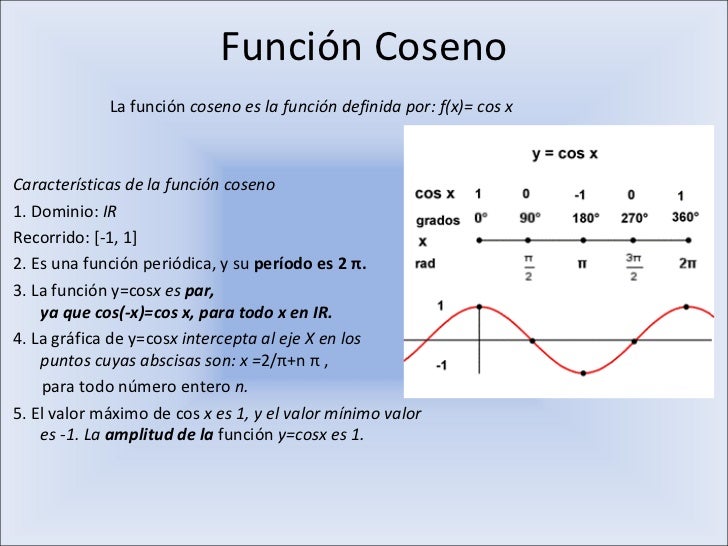
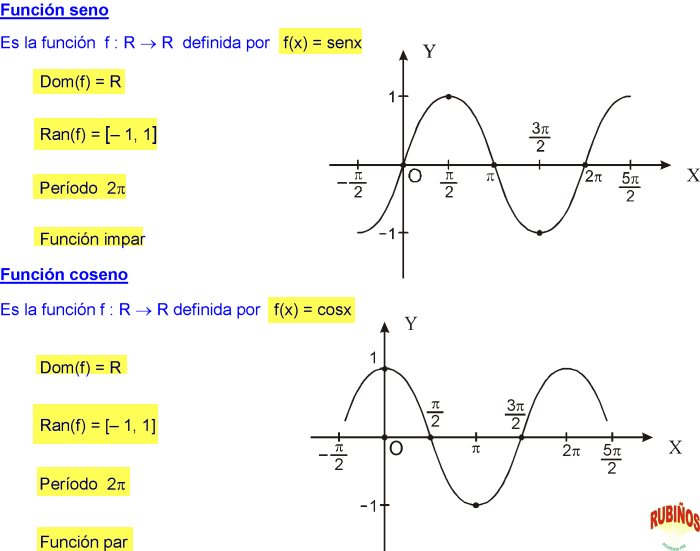
Función trigonométrica: función coseno. Amplitud, periodo y traslación. Propiedades: dominio, recorrido, continuidad, puntos de corte con los ejes, simetría, crecimiento y decrecimiento, máximos y mínimos, periodicidad y acotación. Ejemplo y representación gráfica de la función coseno. Tabla de valores con los ángulos notables.. Las funciones coseno y seno se denominan funciones circulares porque sus valores están determinados por las coordenadas de puntos en el círculo unitario. Para cada número real t, hay un arco correspondiente que comienza en el punto (1, 0) de longitud (dirigida) t que se encuentra en el círculo unitario.

Dominio Y Rango De Coseno rowrich

Funciones trigonométricas

¿Cuál es el dominio de la función coseno? Seleccione una O a. [0, 1] O b. [1, 1] O c. (∞0, ∞0

Calcule el dominio de la función y=(4/senx) +2 YouTube

SAHETO GRÁFICA DE LA FUNCIÓN COSENO

FUNCIÓN SENO COSENO TANGENTE PROBLEMAS RESUELTOS DE DOMINIO RANGO AMPLITUD PERIODO GRÁFICA

funciones trigonometricas FUNCIÓN COSENO

Dominio que hace biyectiva a la función coseno YouTube

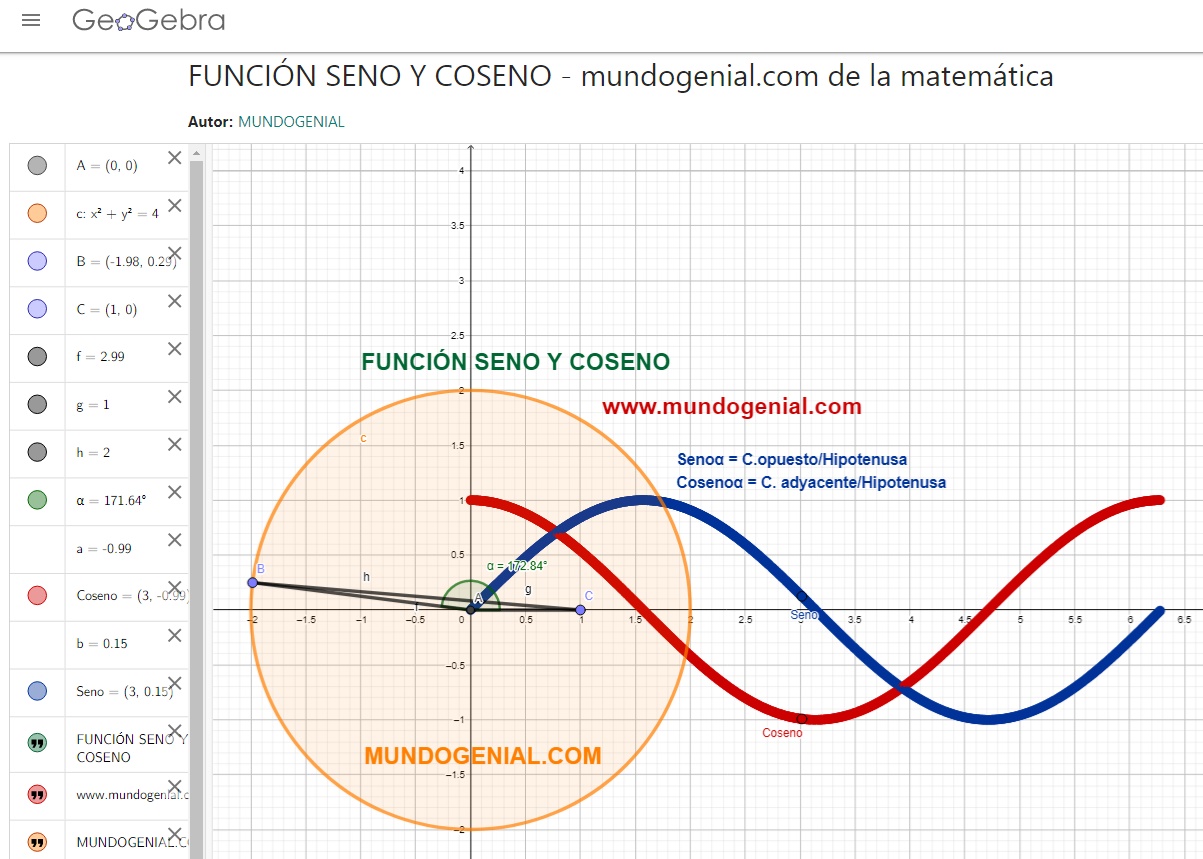
Funciones Seno Y Coseno Funcion Seno Coseno vrogue.co

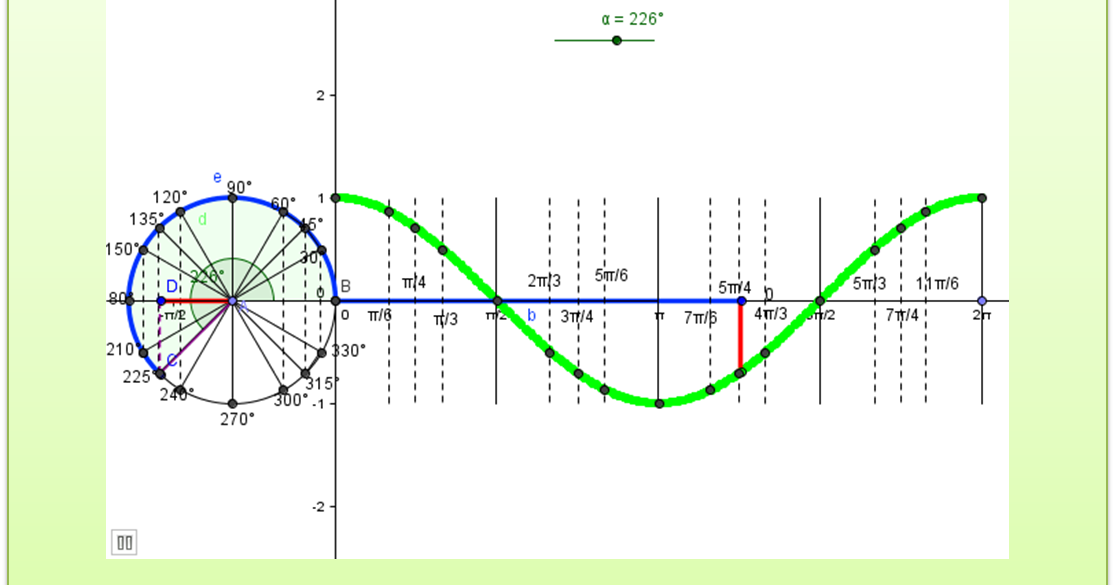
Dominio y Recorrido de la función coseno GeoGebra

Seno y coseno inverso

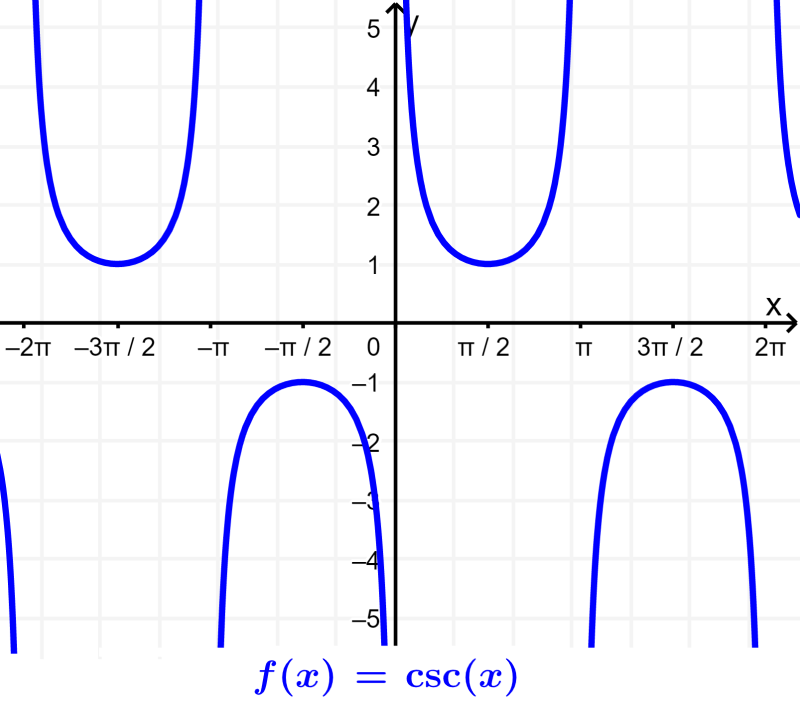
Dominio Y Rango De Coseno rowrich

DOMINIO Y RANGO DE LA FUNCIÓN COSENO YouTube

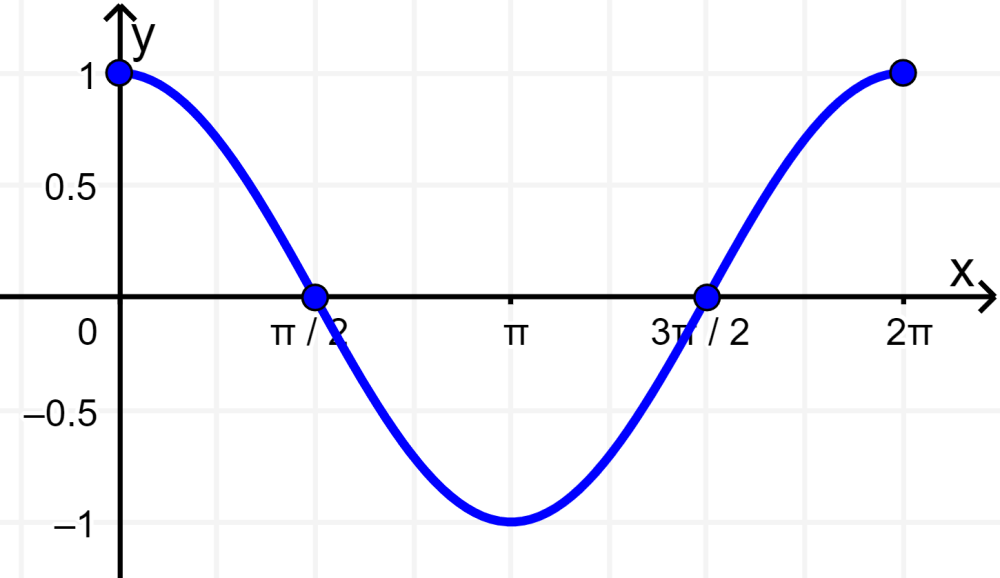
Gráficas de Funciones Trigonométricas Neurochispas

Gráfica De La Función Coseno YouTube

Cálculo del dominio de una función TRIGONOMÉTRICA. Ejercicio 08. YouTube

Dominio de una función. Ejemplos y ejercicios prácticos

Concepto De Dominio Y Rango De Una Funcion Ecer

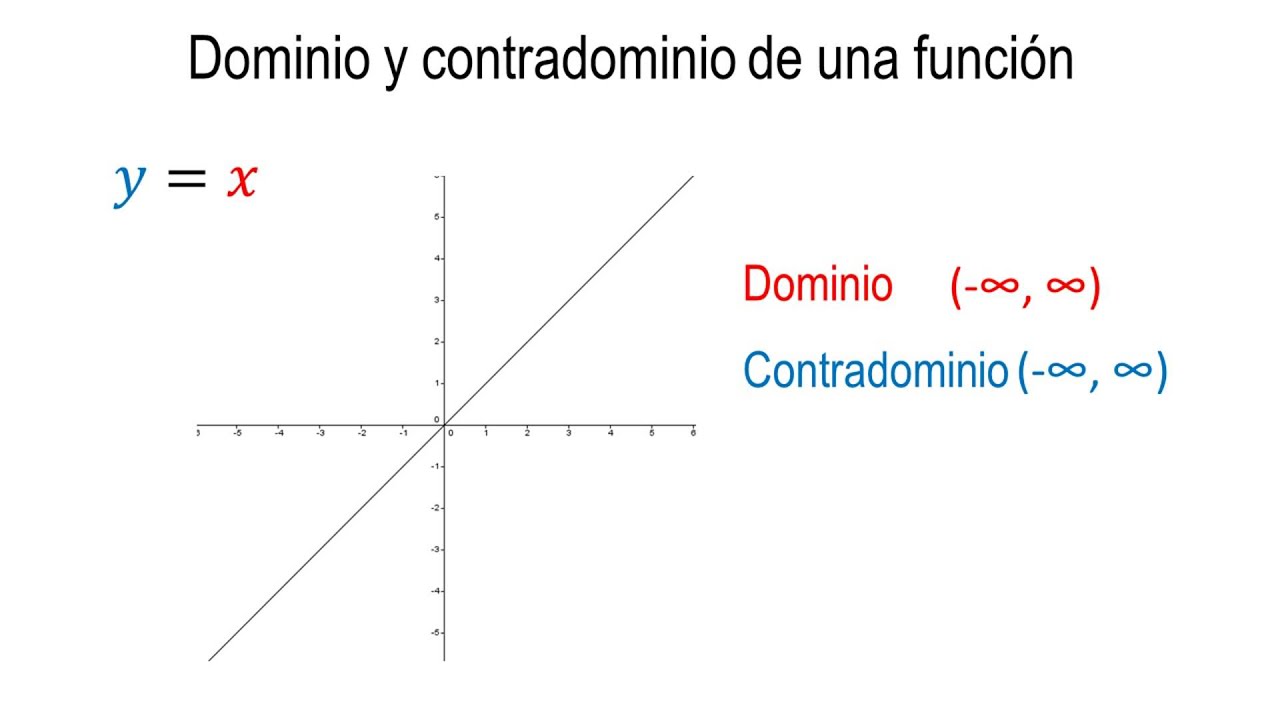
Dominio y Contradominio de una función YouTube

GraficasdelasfuncionesSenoyCoseno

Por tanto, para calcular el dominio de una función racional, debemos encontrar los valores que hacen 0 el denominador y quitárselo a R. Por ejemplo: Esta función existirá siempre, menos cuando el denominador sea igual a 0. Por tanto, debemos encontrar esa restricción que anula al denominador.. Tenemos que el dominio de la función coseno son todos los reales, esto se representa a través del siguiente intervalo: (−∞,∞) En consecuencia, la alternativa b) viene siendo la correcta. ¿Qué es el dominio de una función? El dominio de una función son todos los valores del conjunto de partida, es decir, todos aquellos valores que toma la variable independiente.